A un certain instant du temps de l'univers E2, une "éruption volcanique" au pôle alpha et prenant sa source dans les profondeurs du noyau de l'éther, a provoqué une élévation de la température de l'éther au voisinage de ce pôle. Cette élévation de température a été tellement importante que, par l'énergie tellement considérable ainsi apportée, elle a permis la naissance
1. de toutes les ultra-particules de matière (upm),
2. de toutes les ultra-particules d'antimatière (upam), celles-ci étant moins nombreuses que les upm (on aurait eu le contraire si l'univers avait été créé au pôle omega).
Toutes ces upm et upam se sont éloignées du pôle alpha en suivant les méridiens et les ondes brogliennes qu'elles émettent ont formé une onde SIGMA(tau), sensiblement normale aux méridiens, qui est notre univers E1.
Lorsque cette onde-univers est parvenue dans une zone où la température de l'éther était moins élevée, des associations (upm - upam) se sont produites et, selon les propriétés des ultra-particules concernées, sont nés les photons et les ultra-particules de la matière noire (upmn) et toutes les upam ont alors disparu.
Les upm restantes se sont regroupées pour commencer à former la matière ordinaire telle qu'on la connait, mais ces regroupements ont provoqué un retard (en termes de temps propres) par rapport aux upmn, de sorte que très vite notre univers a acquis la structure suivante :
Onde SIGMA(tau) formée exclusivement de matière noire, très dense et uniformément répartie, suivie de près par la matière ordinaire composant les galaxies. La matière noire attire par gravitation (page 9) les galaxies et tend à réduire leur retard. Inversement une galaxie attire la matière noire "située juste en face" (c-à-dire sur les mêmes méridiens) et y provoque une déformation qui est fonction de la taille de la galaxie. Il est tentant de considérer que l'onde SIGMA(tau) est l’espace-temps de la Relativité Générale.
On peut raisonnablement supposer que la surface de la boule B n'est pas rigoureusement lisse mais qu'elle est "parsemée d'aspérités" (comme les montagnes sur la terre) qui sont à l'origine des premiers regroupements de matière ordinaire.
L'existence des ondes de type L, infiniment plus rapides que la lumière et qui sont les vecteurs de l'information en physique quantique, rend inutile l'hypothése de l'inflation.
L'onde SIGMA(tau) a sensiblement unr forme hyper-sphèrique à 3 dimensions centrée au pôle alpha , et à chaque instant de E2, toutes ses ultra-particules ont (en première approximation) le même temps propre s qui est l'âge de notre univers.
Si la température de l'éther ressemble à celle de l'atmosphère terrestre (ce que nous supposerons): minimale au voisinage des pôles, maximale an niveau de l'équateur, et variant de façon monotone entre ces valeurs extrêmes. il serait possible de résoudre le problème de la constante de Hubble comme le prouve la démonstration suivante.
La constante de Hubble
Les 2 valeurs de la constante de Hubble : 67.8 et 73.5 (km/s)/Mpc posent un problème insoluble aux astrophysiciens puisqu'elles sont incompatibles avec l'existence de la constante de Hubble. Ma théorie résout ce problème en montrant que cette constante est en réalité une fonction très légèrement croissante de l'âge de notre univers.
A un même instant t de E2 considérons 2 points fixes S et S' de l'onde-univers ∑(t) qui, comme tous les points fixes de cette onde, décrivent des méridiens de l'éther et ont le même temps propre s. Désignons par α la mesure de l'angle dièdre qui contient les méridiens décrits par S et S' et dont l'arête est l'axe des pôles α et ω.
Le croquis ci-dessous est une coupe de l'éther par le plan passant par les pôles et le point S. O est le centre de l'éther et R son rayon. Le temps propre s de S est la longueur de l'arc αS.
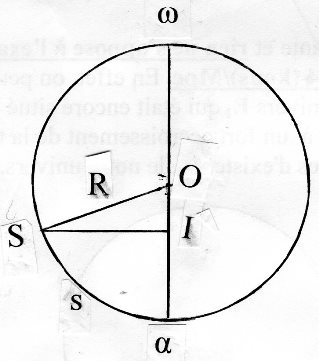
La température de l'éther en S dépend de s : elle sera notée τ (s). Comme notre univers n'a pas encore atteint l'équateur de l'éther, τ (s) est une fonction croissante de s. La vitesse de S, qui est la vitesse de propagation de l'onde ∑(t) ; vaut donc ds/dt = √ τ (s).
Le plus court chemin reliant S et S', dans ∑(t), est un arc de cercle centré en I sur l'axe des pôles ; sa longueur u est la distance de S à S' ; elle vaut
u = α.R.sin(s/R)
La vitesse d'éloignement entre S et S' est
v = du/dt = α.cos(s/R).√ τ (s)
et le paramètre H de Hubble vaut
H = v/u = √ τ (s)/(R.tan(s/R))
H n'est pas une constante et rien ne s'oppose à l'exactitude de chacune des 2 valeurs de H: 67.8 et 73.5 (km/s)/Mpc. En effet, on peut admettre que la valeur 67.8 correspond à un univers E1 qui était encore situé près du pôle α :
H = 67.8
s = 2
T(s) = 18400
et que la valeur actuelle 73.5 est due à un fort accroissement de la température de l'éther pendant les milliards d'années d'existence.de notre univers :
H = 73.5
s = 13.8
T(s) = 1 053 500
____________________________
Extrait de la page 15 :
Considérons la fonction numérique psi de 3 variables réelles t0, R, Z définie par le programme suivant et qui concerne une source lumineuse S' observée par un astronome S.
tS = R.Arcsin[sin(t0/R)/(Z+1)] [cf formule (14,2)]
j = Ln[tg(t0/2R)] – Ln[tg(tS/2R) [cf formule (14,1)]
d = j.R.sin(t0/R) [distance actuelle en Gal]
psi(t0, R, Z) = d
R =35
to = 13.8
Z : décalage spectral
ts : âge de l'univers à l'émission de la lumière reçue
j : distance angulaire
d : distance actuelle
Calculs très faciles sur Excel
héoriquement les calculs effectués avec des Z < 0.5 sont exacts avec une incertitude < 3 %


