La matière ordinaire, dont la densité est beaucoup plus faible, est située au voisinage de SIGMA(tau) et présente un léger retard sur celle-ci (retard qui sera négligé dans cette page et les suivantes).
a) Propagation des ondes gravitationnelles – C’est l’attraction gravitationnelle mutuelle entre les upmn qui crée une tension à l’intérieur de l'onde SIGMA(tau) permettant la propagation des ondes gravitationnelles selon les prévisions de la Relativité Générale.
b)Tout quanta (donc tout photon) possède une trajectoire absolue qui, loin de toute galaxie, coupe les méridiens de l'éther sous un angle de 45°.
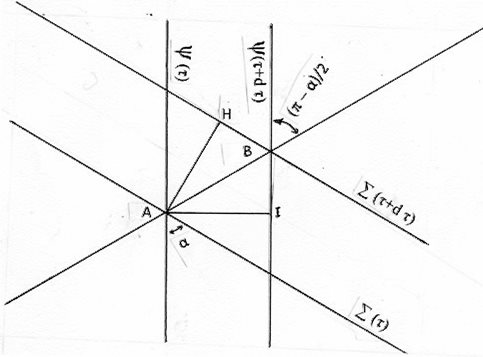
Ce croquis représente le plan parallèle aux méridiens qui contient les positions A et B d'un photon aux dates tau et tau + d.tau du temps de l'univers E2. Ont été dessinées les traces, à ces 2 dates, de l'onde brogienne PSI associée à ce photon, onde qui est parallèle aux méridiens (page 8), et celles de l'onde-univers SIGMA qui fait un angle alpha avec les méridiens. H et I sont les projections orthogonales du point A sur les traces de SIGMA et de PSI à la date tau+d.tau. Comme localement toutes les ondes de type S se propagent à la même vitesse dans l'éther, AH = AI et par suite HB = IB. Or H est la position du point A à la date tau + d.tau, et par suite HB est le chemin parcouru par le photon pendant le temps d.tau. IB est le temps propre (mesurable par un observateur) qu'a duré ce parcours, et relativement à l'onde SIGMA, la vitesse du photon est donc :
HB /BI = 1 mètre/mètre-temporel ou c m/s
(1 seconde = c mètres-temporels où c = 299792458)
Loin des galaxies, l'onde SIGMA est ortogonale aux méridiens :(1 seconde = c mètres-temporels où c = 299792458)
alpha = pi/2, et la trajectoire AB du photon fait avec les méridiens l'angle (pi - alpha)/2 = pi/4. C'est ce résultat capital qui permet à ma théorie le calcul de la distance d'une source lumineuse très éloignée en fonction du seul décalage spectral de la lumière reçue (voir les pages 14 et 15).
