Deux observateurs X et Y utilisent respectivement les repères orthonormés (O i j k) et (O' i j k), l'origine O' décrivant l'axe (O i) à la vitesse constante v. L'observateur X attribue à un événement ponctuel (e) des coordonnées (x, y, z) et une date t. L'observateur Y attribue au même événement (e) des coordonnées (x', y', z') et une date t' données par les formules de Lorentz
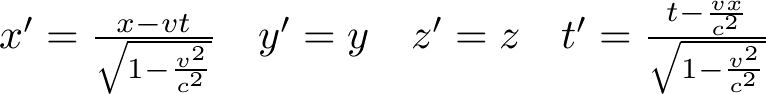

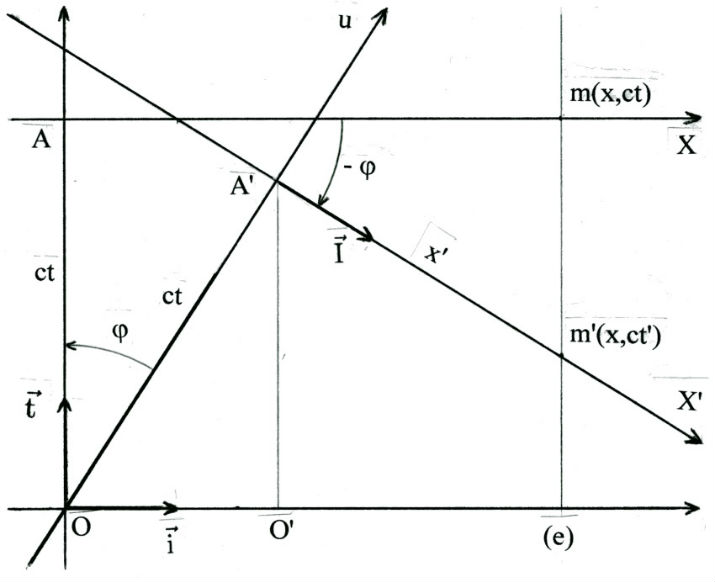
D'après les formules précédentes, ce point m' a pour abscisse x et pour ordonnée ct'. Cette construction, effectuée pour phi = 0, conduit aux points A(0,ct) et m(x,ct).
Supposons que l'événement (e) se produise en un point qui soit fixe par rapport au repère (O' i j k) : alors t' représente son temps propre. Or les temps propres ont une valeur intrinsèque ; l'ordonnée ct' du point m' a donc une valeur intrinsèque et il est assez naturel de supposer qu'il en est de même des grandeurs caractérisant les autres éléments du plan (O i t) et que l'espace E n'est pas une simple abstraction mathématique mais qu'il possède une existence réelle.
Dans cette hypothèse, le repère utilisé par l'observateur Y n'est pas le repère (O' i j k) mais le repère (A' I j k) et l'espace, défini par ce repère et dans lequel opère cet observateur, a l'apparence d'une onde puisqu'il se propage à la vitesse de la lumière dans l'espace E rapporté au repère (O i j k t) et muni du temps t. Il en est de même pour l'observateur X dont l'espace mobile, défini par le repère (A i j k), est coupé par le plan de la figure suivant la droite AX.
De plus, il apparaît que la direction de l'axe (O, t) est une direction privilégiée de l'espace E, chacun des observateurs localisant l'événement ponctuel (e) au point de son propre espace mobile où (e) se projette parallèlement à cette direction privilégiée (en m pour l'observateur X, en m' pour l'observateur Y, si y = z = 0). Enfin l'étude du cas limite où v = c, soit phi = pi/2, montre que les ondes lumineuses sont parallèles à cette direction privilégiée.
Convaincu de l'existence physique de cet espace euclidien E à 4 dimensions, j'ai voulu en entreprendre l'étude à l'aide d'une algèbre de Clifford. N'en connaissant aucune qui soit vraiment adaptée à cette étude, j'ai dû en créer une mais quelle ne fut pas ma déception quand j'ai découvert que celle-ci conduisait à un espace euclidien n'ayant pas 4 mais 5 dimensions ! (voir annexe B). Finalement j'ai dû me résoudre à l'idée que l'espace E, qui contient notre univers E1, est une partie d'un univers E2 à 5 dimensions qui est lui-même inclus dans des univers de dimensions supérieures, la construction d’une théorie cohérente du monde physique semblant ainsi exiger l’adjonction d’un troisième infini à l’infiniment petit et à l’infiniment grand : l’infini des dimensions.
Si notre univers est effectivement inclus dans un univers à 5 dimensions, de nombreuses énigmes s'en trouvent immédiatement résolues ; en particulier le problème de l'avant big-bang disparaît et le principe de relativité devient évident, notre univers ayant été créé dans un univers qui existait déjà et dont les lois sont évidemment les mêmes pour tous les observateurs.
Mais comment construire une physique applicable à un tel univers à 5 dimensions qui est totalement inconnu et inaccessible ? La seule façon raisonnable de procéder semble être de supposer que cet univers possède une structure analogue à celle de notre univers, que les notions fondamentales, telles que le temps ou l'énergie, ont encore un sens dans un tel univers et que la plupart des lois les plus élémentaires de la physique lui sont applicables. C’est cette méthode que j’ai utilisée pour construire la présente théorie.
