On conserve les notations de la page précédente. Le but de ce paragraphe est le calcul, effectué par un observateur O, de la distance actuelle d'une galaxie contenant une source très lumineuse S. L'onde
SIGMA(tau), qui est notre univers, a actuellement un rayon ρ = R.sin(t0/R) où to est l'âge actuel de notre univers et R le rayon de l'éther (cf page 10).
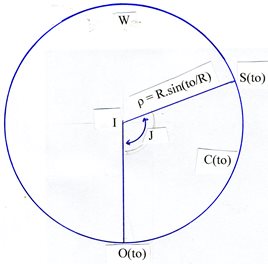
Ce croquis représente le cercle C(to) qui est la section, par l’hyperplan H de E2 qui contient la position actuelle de notre univers, de la sphère ordinaire W sur laquelle se sont propagés les photons issus de S et reçus par l'observateur O (voir page 14). I est le centre de ce cercle, S(to) et O(to) les positions actuelles de S et de O. Comme H est orthogonal à l’axe des pôles alpha-omega, les 2 rayons IS(to) et IO(to) constituent une section droite de l’angle dièdre formé par les méridiens trajectoires dans l'éther de S et de O et l'angle qu'ils définissent vaut j radians.
La trajectoire dans l'éther d'un photon est "matérialisée" par les upmn qu'il a rencontrées. Les upmn, qui ont ainsi "matérialisé" les trjajectoires de tous les photons émis par S et reçus en O, se sont déplacées sur leurs trajectoires respectives (méridiens) et se retrouvent actuellement sur l'arc S(to)O(to) du cercle C(to). qui mérite le nom de position actuelle des trajectoires des photons concernés. Sa longueur est d'ailleurs la plus courte distance séparant, actuellement dans notre univers, les postiions de S et de O : c'est la distance actuelle d de S à O qui vaut donc
d = ρ.j = j. R.sin(t0/R).
Considérons la fonction numérique psi de 3 variables réelles t0, R, Z définie par le programme suivant :
tS = R.Arcsin[sin(t0/R)/(Z+1)] [cf formule (14,2)]
j = Ln[tg(t0/2R)] – Ln[tg(tS/2R) [cf formule (14,1)]
d = j.R.sin(t0/R) [distance actuelle en Gal]
psi(t0, R, Z) = d
Il est clair que, si t0 est l’âge actuel de l’univers et R le rayon de l’éther, psi(t0, R, Z) représente la distance actuelle d à notre galaxie d’une source éloignée S dont la lumière présente le décalage spectral Z. La valeur 13.8 semblant faire consensus pour l'âge actuel to de l'univers, il suffit donc de connaître la valeur du rayon R de l'éther pour calculer la distance d à partir du décalage Z.
La méthode choisie pour déterminer la valeur de R fait intervenir la constante de Hubble Ho = v/d où d est la distance actuelle à notre galaxie d'une source S et v sa vitesse d'éloignement. En supposant que la formule Z+1 = racine carrée de (c+v)/(c-v) soit applicable (effet Doppler-Fizeau relativiste), on trouve
v = c(u-1)/(u+1) où u = (Z+1)².
Il est donc possible de calculer Ho en fonction de tout couple (Z,R), si l'on admet que to = 13.8On sait que 2 valeurs de Ho divisent actuellement les cosmologistes
- la valeur 67.8 issue du CMB par Planck
- la valeur 73.5 calculée par l'équipe d'Adam Riess
En effectuant le calcul de Ho selon le programme précédent pour un très grand nombre de valeurs possibles du couple (Z, R), on constate que les valeurs trouvées sont beaucoup plus proches de la valeur 67.8 que de la valeur 73.5. C'est donc le nombre 67.8 qui semble être, selon ma théorie, la bonne valeur de la constante de Hubble.
Calcul du rayon R de l'éther - La méthode utilisée consiste à :
1) construire une liste L de valeurs de Z, allant de 0 à 0.25 et formant une suite arithmétique de raison 0.0025
2) choisir une valeur pour R et, pour chaque Z de la liste L,
calculer :
- a) la distance d = psi(to , R, Z) (to = 13.8);
- b) d' = d/0.003262 (distance en Mpc) ;
- c) la vitesse d'éloignement V d'une source S correspondant à ce Z ;
- d) H = V/d' (Hubble) ;
- e) la différence entre H et Ho (= 67.8) ;
- f) la plus grande de ces différences, notée MAX(R) ;
3) Déterminer la valeur R(to,Ho) de R qui donne à MAX(R) la plus petite valeur possible notée MIN(to,Ho).
Excel est excellent pour ces calculs. J'ai trouvé (par une variante de la méthode indiquée) : R(to,Ho) = 38.06 Gal et MIN(to,Ho) = 0.16. C'est cette valeur de R qui fournit donc le meilleur accord possible entre ma théorie et la valeur 67.8 de Ho pour les distances < 3 Gal. Ce nombre 38.06 Gal doit être considéré comme étant le rayon de l'éther.
ADDITIF (mars 2021)
Quelle ne fut pas ma surprise ,il y a quelques années, quand j'ai découvert que pour certaines valeurs du rayon de l'éther ma théorie attribuait à la constante de Hubble des valeurs très proches du nombre 67.8. Ce résultat inattendu m'a rassuré sur la solidité des bases de ma théorie, confirmant ainsi l'extraordinaire puissance des mathématiques pures dans la recherche de la strcture profonde de l'univers.
Mais je viens de découvrir que la méthode de calcul du rayon R de l'éther que je viens d'exposer permet de calculer la constante de Hubble Ho, avec une très grande précision, à partir de la seule valeur to de l'âge de l'univers : il suffit de rechercher la valeur de Ho qui donne à MIN(to,Ho) sa valeur minimale. Cette recherche peut être effectuée, d'abord parmi les nombres entiers, puis parmi les nombres à 1 décimale, puis à 2 décimales, etc... (méthode des approximations successives). Voici les résultats obtenus pour to = 13.77
décimales recherche : début, zone à explorer résultat
0 < 66 65 66 … 67
1 67 - 0,1 66.9 67.0 67.1 … 67.4
2 67.4 - 0.01 67.39 67.40 67.41 … 67.42
Les résultats obtenus pour les valeurs de to comprises entre 13.7 et 13.9, sont consignés dans les 4 premières colonnes du tableau suivant
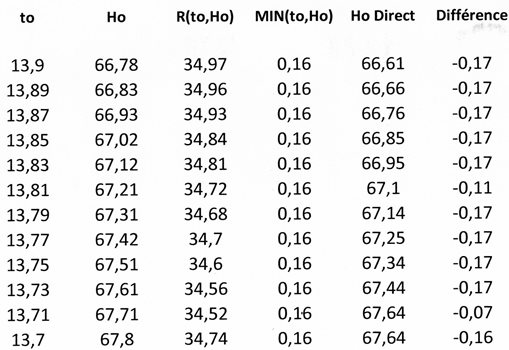
La non-nullité de Min(to,Ho) traduit le fait que, même pour les "petites" ditances dont le décalage spectral Z est < 0.25, Ho n'est une constante qu'à 0.16 unité près (soit 0.2 %). On constate que, pour cette tranche d'âges de 200 millions d'années, le rayon R = R(to,Ho) de l'éther est bien une constante (à 1% près) ; le contraire aurait évidemment invalidé ma théorie. La légère croissance observée indique peut-être que, comme sur la terre, les méridiens de l'éther ne sont pas exactement des demi-cercles ???
Calcul pratique deq grandes distances - Pour les calculs concernant une source lumineuse S dont le décalage Z est connu, il suffit d'appliquer les 3 formules indiquées au début de ce paragraphe :
tS = R.Arcsin[sin(t0/R)/(Z+1)] (âge de l'univers à l'émission en Ga)
j = Ln[tg(t0/2R)] – Ln[tg(tS/2R) (distance angulaire en radians)
d = j.R.sin(t0/R) (distance actuelle en Gal)
où to = 13.77 Ga et R = 34.7 Gal
Voici ce qu'on obtient pour la galaxie ZN-z11 (z = 11.09) :
âge de l'univers à l'émission ts = 1.109 Ga
distance angulaire J = 2.532 rd = 145 °
distance actuelle d = 33.954 Gal
distance à l'émission = 2.808 Gal
Conclusion - J'aimerais savoir pourquoi l'hypothèse de l'existence d'un univers physique contenant notre univers n'a jamais été étudiée par les astrophysiciens. Pourriez-vos me renseigner ? Merci d'avance.
Pierre Sigaud
Prof de Math Sup honoraire
au lycée Champollion de Grenoble
psigaud@free.fr
U
Ga
